 ,
G. Berthomieu
,
G. Berthomieu ,
J. Provost
,
J. Provost ,
E. Fossat
,
E. Fossat
Previous: Th. Corbard's page
Th.Corbard  ,
G. Berthomieu
,
G. Berthomieu ,
J. Provost
,
J. Provost ,
E. Fossat
,
E. Fossat
(1) Laboratoire G.-D.Cassini, Observatoire de la Côte d'Azur, Nice
(2) Département d'Astrophysique, UNSA, Nice
The solar core rotation is investigated by means of a 2D
regularized least square inversion.
A reliable rotation rate above
The LOWL data contain 1102 modes
This figure is a
An observable consequence of the solar rotation is that the azimuthal degeneracy
of global modes of oscillation is raised. The rotational splitting is
defined by :
where
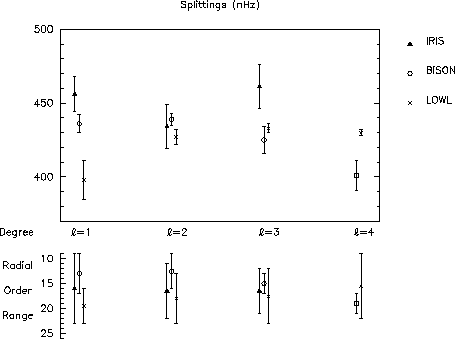
This figure gives some recent results obtained by various groups for the low l degree
rotational splitting frequencies. The value of the splitting corresponds to
an average over the given radial order range assuming that all the splittings for a given degree
l are measuring the same quantity. The weighting coefficients used to compute the mean
splitting values have been used in the inversion process too.
For low rotation the frequency shifts are
given by:
where
We search for the unknown rotation as a linear combination of piecewise polynomials,
projected on a tensorial product of B-spline basis (Corbard et al., 1996). We take into
account the observational
errors (with standard deviation
The regularization parameters
The inversion depends on the number of piecewise polynomials, on the order of the spline
functions and on the distribution of the break points of these polynomials. In what follows, the distribution of these points along the radius has been chosen according to the density of the turning
points of the considered p-modes for a given dataset.
A complete description of the method and the choice of the parameters used for inverting
LOWL data can be found in Corbard et al. (1996)
 is obtained by
using the rotational splittings measured between 1994 and 1996
with the data of the LOWL instrument wich can observe both
low and intermediate degree p-modes. For sounding
the deeper layers, we have alternately added the most recent
published splittings of the IRIS and the BiSON network groups.
These two sets have been known to be inconsistent at more than
a 3-sigma level. The consequences of this difference on the
behaviour of the rotation rate inside the solar core, seen by
the global inversion, are studied and discussed in this poster.
is obtained by
using the rotational splittings measured between 1994 and 1996
with the data of the LOWL instrument wich can observe both
low and intermediate degree p-modes. For sounding
the deeper layers, we have alternately added the most recent
published splittings of the IRIS and the BiSON network groups.
These two sets have been known to be inconsistent at more than
a 3-sigma level. The consequences of this difference on the
behaviour of the rotation rate inside the solar core, seen by
the global inversion, are studied and discussed in this poster.
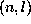 with degrees up to l=99 and
frequencies lower than
with degrees up to l=99 and
frequencies lower than 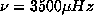 . For each mode, individual
splittings are given by, at best, three a-coefficients of their expansion on orthogonal
polynomials defined by Schou et al. (1994).
. For each mode, individual
splittings are given by, at best, three a-coefficients of their expansion on orthogonal
polynomials defined by Schou et al. (1994).
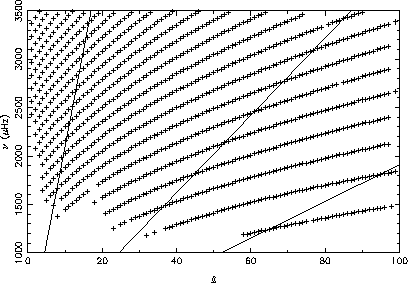
 diagram showing the modes included in the LOWL
2 years dataset. Solid lines indicate the value of
diagram showing the modes included in the LOWL
2 years dataset. Solid lines indicate the value of 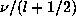 that correspond
to modes with turning points
that correspond
to modes with turning points 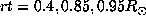 from the left to the right.
from the left to the right.

 denotes the frequency of the mode of degree l, radial order n
and azimuthal order m.
denotes the frequency of the mode of degree l, radial order n
and azimuthal order m.
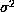 ) average over n of
the splittings obtained for each mode
) average over n of
the splittings obtained for each mode 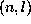 by Chaplin et al. (1996) from the 16-month power spectrum.
by Chaplin et al. (1996) from the 16-month power spectrum.
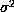 )
average over n of the a1 coefficients obtained for each mode
)
average over n of the a1 coefficients obtained for each mode 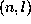 .
In the minimization process, individuals splittings
have been built from the given a-coefficients and the weighting coefficients
have been taken as the inverse of uncertainties on the individual splittings which have been
calculated by assuming them uncorrelated and independent of m for each
.
In the minimization process, individuals splittings
have been built from the given a-coefficients and the weighting coefficients
have been taken as the inverse of uncertainties on the individual splittings which have been
calculated by assuming them uncorrelated and independent of m for each  and such
that they lead at best (in least-squares sense) to the quoted errors given on the a-coefficients.
By this way a weigthed average over n and m of these individual splittings leads to
the same values and errors as the ones shown on the figure for l=1,2,3,4.
and such
that they lead at best (in least-squares sense) to the quoted errors given on the a-coefficients.
By this way a weigthed average over n and m of these individual splittings leads to
the same values and errors as the ones shown on the figure for l=1,2,3,4.
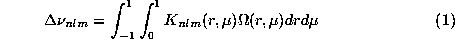
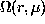 is the unknown rotation rate versus depth and latitude,
is the unknown rotation rate versus depth and latitude,
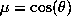 ,
, 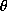 is the colatitude and r the normalized solar radius. The kernels
is the colatitude and r the normalized solar radius. The kernels 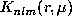 depend on the model
and the eigenfunctions of the mode which are assumed to be known exactly
(e.g. Christensen-Dalsgaard & Berthomieu 1991).
depend on the model
and the eigenfunctions of the mode which are assumed to be known exactly
(e.g. Christensen-Dalsgaard & Berthomieu 1991).
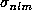 ) and a regularization term to avoid the large
spurious variations of the solution induced by the ill-conditioned inversion problem. Thus we
search coefficients that represent the projection of the rotation rate on the chosen B-splines
basis by minimizing:
) and a regularization term to avoid the large
spurious variations of the solution induced by the ill-conditioned inversion problem. Thus we
search coefficients that represent the projection of the rotation rate on the chosen B-splines
basis by minimizing:
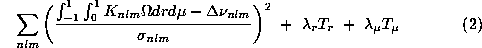
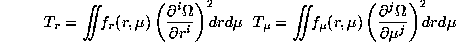
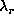 and
and 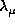 and functions
and functions 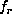 and
and 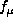 are used to define the trade off
between the resolution and the propagation of the input errors. We can choose any derivative
of the rotation rate. This leads to different behavior of the rotation especially at
locations where
the observed modes are not enough to constrain the solution. For the results discussed here we
choose
are used to define the trade off
between the resolution and the propagation of the input errors. We can choose any derivative
of the rotation rate. This leads to different behavior of the rotation especially at
locations where
the observed modes are not enough to constrain the solution. For the results discussed here we
choose 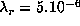 ,
, 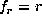 , i=2 and
, i=2 and 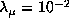 ,
, 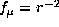 , j=1 .
, j=1 .
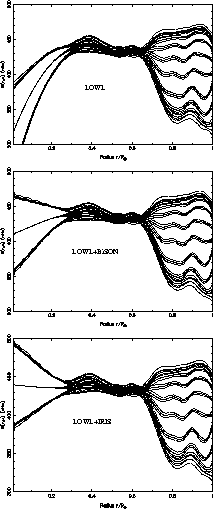
 ) obtained by inverting
LOWL data, LOWL+IRIS data and LOWL+BiSON data. The 3 solutions differ
only under 0.2
) obtained by inverting
LOWL data, LOWL+IRIS data and LOWL+BiSON data. The 3 solutions differ
only under 0.2  and show no latitudinal dependencies below
this depth. The solution obtained between 0.4 and
and show no latitudinal dependencies below
this depth. The solution obtained between 0.4 and  is discussed in Corbard et al. (1996).
is discussed in Corbard et al. (1996).
 LOWL data are compatible within 1
LOWL data are compatible within 1  error bars with a core that
rotate slower than the radiative interior.
error bars with a core that
rotate slower than the radiative interior.
 Solutions
with IRIS and BiSON data are compatible and show that an extension to the solar core of
the rather uniform rotation
found in the outer radiative interior could explain the observed splittings.
Solutions
with IRIS and BiSON data are compatible and show that an extension to the solar core of
the rather uniform rotation
found in the outer radiative interior could explain the observed splittings.
The difference between LOWL and IRIS or BiSON data (especially for l=1)
is sufficient to produce solutions that are not compatible. This is not surprising since
these depths are intrinsically not well constrained so that little variation
in the data could produce important variation in the solution.
Nevertheless all the available observations argue against theories for
angular momentum transport which predict
a rotation rate at 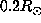 very higher than the equatorial rotation rate.
very higher than the equatorial rotation rate.
Although the 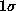 error bars shown on the figure are large below
error bars shown on the figure are large below
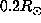 , we can not insure that the true rotation rate lies inside
these error bars. In fact these bars represent the uncertainties on a weighted
averaged of the rotation rate. In an attempt to have a best interpretation of our
results we must have a look at the weighting function given by
the so-called averaging kernels.
, we can not insure that the true rotation rate lies inside
these error bars. In fact these bars represent the uncertainties on a weighted
averaged of the rotation rate. In an attempt to have a best interpretation of our
results we must have a look at the weighting function given by
the so-called averaging kernels.
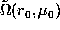 at a
point (
at a
point (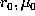 ) is obtained as a linear combination of the
data
) is obtained as a linear combination of the
data 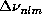 . Thus from Eq.(1) it follows that averaging kernels
. Thus from Eq.(1) it follows that averaging kernels 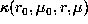 ,
which are a linear combination of rotational kernels
,
which are a linear combination of rotational kernels 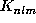 , exist such that:
, exist such that:
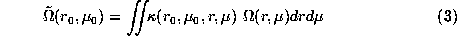
The radial and latitudinal full widths at mid height (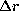 and
and
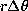 ) of these kernels provide an estimation of the spatial resolution of the
inversion at a point
) of these kernels provide an estimation of the spatial resolution of the
inversion at a point
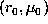 . It increases with lower regularizing term, at the expense of larger errors on
the solution.
. It increases with lower regularizing term, at the expense of larger errors on
the solution.
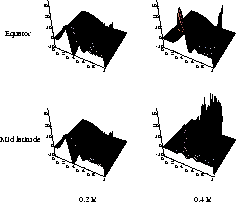
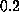 and
and 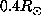 at the equator and mid latitude.
at the equator and mid latitude.
The radial and latitudinal resolution reached at 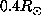 at the equator
are respectively
at the equator
are respectively
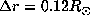 and
and 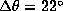 . Nevertheless, we obtain a lot of
additional peaks localized at the surface. Generally, a well peaked kernel can be obtained
only if a large amount of cancelations eliminates the dominant contribution of the
rotational kernels near the surface. In this inversion the cancelation is not completely done
showing that a better inversion should require observation of high degree modes which
are able to give informations about zones near the solar surface. We note however that
the peaks shown near the surface remain unresolved with the grid used for the plot
and that their contribution to the whole kernel is very small.
. Nevertheless, we obtain a lot of
additional peaks localized at the surface. Generally, a well peaked kernel can be obtained
only if a large amount of cancelations eliminates the dominant contribution of the
rotational kernels near the surface. In this inversion the cancelation is not completely done
showing that a better inversion should require observation of high degree modes which
are able to give informations about zones near the solar surface. We note however that
the peaks shown near the surface remain unresolved with the grid used for the plot
and that their contribution to the whole kernel is very small.
Although the two kernels at 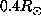 are well localized, the two ones at
are well localized, the two ones at 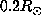 are not distinguishable
and are both localized at the equator and
are not distinguishable
and are both localized at the equator and 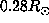 . This result shows
that our inversion is not able to detect a latitudinal dependency of the rotation rate
even if one exists at
. This result shows
that our inversion is not able to detect a latitudinal dependency of the rotation rate
even if one exists at 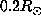 . The solution obtained at all latitudes below 0.3
. The solution obtained at all latitudes below 0.3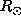 is an estimation of the rotation rate in the equatorial plane.
A more important problem arise from the fact that the averaging kernels calculated at
is an estimation of the rotation rate in the equatorial plane.
A more important problem arise from the fact that the averaging kernels calculated at
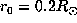 and below this depth are still localized between 0.25 and 0.28
and below this depth are still localized between 0.25 and 0.28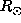 .
This indicates that the true rotation rate at a target location below 0.2
.
This indicates that the true rotation rate at a target location below 0.2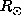 contributes only for a few part in the calculation of the inferred rotation rate at this
location.
contributes only for a few part in the calculation of the inferred rotation rate at this
location.
The solutions we obtain show that the different
values given by observers for the low l splittings lead to
different behaviours of the inferred rotation rate in the core.
Therefore the inversion is sensitive to the actual observational differences.
Nevertheless the shape of the averaging kernels corresponding to solar core layers
makes the interpretation of results
in term of the true rotation rate very difficult.
For example,
the averaging kernel calculated at 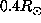 presents important oscillations
up to
presents important oscillations
up to 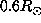 . Therefore the interpretation of the value of the rotation
rate obtained at
. Therefore the interpretation of the value of the rotation
rate obtained at 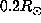 depends strongly on the behavior of the rotation rate
in the radiative interior. We note however that the integral of the averaging
kernel between
depends strongly on the behavior of the rotation rate
in the radiative interior. We note however that the integral of the averaging
kernel between 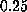 and
and 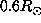 is null. Thus, if we suppose that the rotation
rate is constant in the radiative interior and down to
is null. Thus, if we suppose that the rotation
rate is constant in the radiative interior and down to 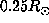 , we can interpret
the value obtained at
, we can interpret
the value obtained at 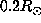 as a weighted averaged of the true rotation rate
between 0.1 and
as a weighted averaged of the true rotation rate
between 0.1 and 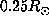 the weighting function being the corresponding part of
the averaging kernel. Nevertheless although the solid rotation found between
the weighting function being the corresponding part of
the averaging kernel. Nevertheless although the solid rotation found between 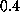 and
and 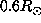 is thought to be reliable, its extension down to 0.25
is thought to be reliable, its extension down to 0.25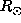 is more speculative
and some little gradients in these zones can modify significantly the interpretation
of the value of the rotation rate found at
is more speculative
and some little gradients in these zones can modify significantly the interpretation
of the value of the rotation rate found at 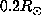 and deeper.
and deeper.
A better understanding of the rotation of the core should require a better agreement between the different analysis of the different observations. However, this work shows some limits in the utilization of a 2D RLS code to probe the rotation of the core. Some other global inversion techniques as SOLA should be helpful by searching explicitly averaging kernels without any negative part. Such kernels, even larger than those obtained in this work should be useful to complete the interpretation of our results in the core.
References
Chaplin W.J., Elsworth Y., Howe R., 1996, Solar core rotation: low-degree solar p-mode rotational splitting results from BISON, MNRAS, submitted
Christensen-Dalsgaard J., Berthomieu G., 1991, Theory of Solar Oscillations.
In: Cox A.N., Livingstone W.C., Matthews M.S. (eds)
Solar Interior and Atmosphere. Univ. of Arizona Press, Tucson, p. 401
Corbard T., Berthomieu G., Provost J. and Morel P., 1996,
The solar rotation rate from LOWL data:
A 2D regularized least-squares inversion using B-splines, 1996, to be submitted to A&A
Gelly B., Fierry-Fraillon D. et al., 1996, submitted to A&A
Gizon L., Fossat E., Lazrek M. et al., 1996,
New IRIS constraints on the solar core rotation,
submitted to A&A Letters
Lazrek M., Pantel A., Fossat E., et al., 1996,
Is the solar core rotating faster or slower the the envelope?, Sol. Phys., 166, 1
Schou J., Christensen-Dalsgaard J., Thompson M.J., 1994,
On comparing helioseismic
two-dimensional inversion methods, ApJ 433, 389
Tomczyk S., Schou J., Thompson M.J., 1995b,
Measurement of the Rotation Rate in the Deep Solar Interior, ApJ 448, L57
Thierry Corbard
E-mail:
corbard@obs-nice.fr
Fax: (+33) 04 92 00 31 21
Dernières modifications: 16 Octobre 1996